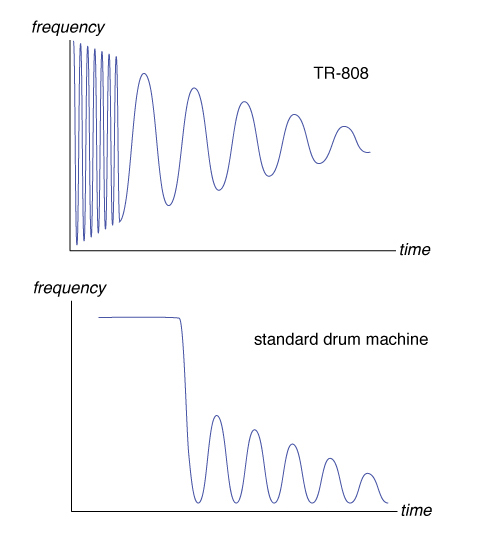
Introduced in the 1980’s, the TR-808 was the first programmable drum machine. You’re unwittingly familiar with sound of the TR-808; it’s featured in more hit songs than Pharell. The 808 is literally THE sound of the 80’s including those synthed beats from Afrika Bambaataa and the Soul Sonic Force’s Planet Rock . The sounds of 808 are iconic; the deep bass, kick drum; the tinny handclaps; the ticky snare; the tishy high hat; that spacey cowbell. Modern rap and hip-hop from the South, aka The Dirty South, continue to be influenced by the TR-808. Consider Outkast’s The Way You Move, it’s deep bass and addictive high hat are classic 808.
Speakerbox vibrate the tank, make it sound like aluminum cans in the back
But I know y’all wanted that 808 can you feel that B-A-S-S, bass
The machine’s affordability, a steal at $1195, and ease of use lead to its original popularity. However only 12,000 TR-808’s were ever made—the last in 1983. Securing a TR-808 today requires about $4,000 and hours entrenched in eBay bidding wars. Subsequently, most of those iconic 808 sounds in today’s music are recorded sounds, samples, not the actual drum machine itself. But the heroic efforts of one resolute Stanford University graduate student are giving this 80’s drum machine new life with an unlikely tool—mathematical theory.
The TR-808 was the last important analog drum machine ever made. The insides of the machine are a complicated mix of circuits with capacitors and resistors working to change the voltage, the signal that produces the sound. Some of these circuits are mundane, but others represent true innovations by Roland, the 808’s manufacturer. Other drum machines produce the sound of a kick drum with a band pass filter that cuts the high and low parts of the frequency leading to a very narrow and sharp wave oscillating at a signal frequency, with the oscillation eventually dying out. In the 808 the punch of that low kick drum is unique; produced by replicating the physical process of a real bass drum. Right after the start of the sound, the frequency of the oscillation is increased for a few milliseconds and then drops down again. The frequency is then allowed to drift and oscillate a minute producing a sighing sound. This sequence creates a very complicated trajectory during which the note evolves across a wide array of pitches. The complex kick drum sound of the TR-808 is accomplished with a complicated type of circuit, a Bridged-T, and therein lies the problem with mathematically modeling it’s sound.
At the top of a hill on the far south side of the Stanford campus sits The Knoll. Formerly home of the university’s president, the Knoll now houses the Center for Computer Research in Music and Acoustics (CCRMA, pronounced “karma”). Here, a dozen faculty and a few dozen graduate students research everything from digital musical composition, to hardware and software, to psychoacoustics. The interior of the late 1800’s Spanish influenced mansion is a combination of recognizable instruments, computer workstations, and hacked-together Franken-equipment mashing the two together. On the second floor, Ph.D. student Kurt Werner is stretching a field of mathematics to reproduce the TR-808 sound. Werner, is the perfect person for the task—bachelors degrees in control systems engineering and music theory from the University of Illinois Urbana Champaign; a hobby of hacking the hardware or “circuit bending” of old musical machines; an interest in experimental electronic composition; and an unrivaled need to share the TR-808 love.
Werner’s research seeks to extend the mathematical field of Wave Digital Filter Theory. The TR-808 is simply a filter in which a voltage signal is passed through and altered to produce sound. A digital filter likewise takes one sequence of numbers and produces another sequence of numbers. Wave Digital Filter Theory, developed by Alfred Fettweis in the late 1960’s, simply tries to translate the filtering done by circuits composed of inductors, capacitors, resistors, diodes, transformers, and so on into filtering done by a set of equations. Through this mathematical transformation, the beloved sounds of analog devices, like the TR-808, can be replicated to modern digital machines. Wave Digital Filter Theory is not new to the music industry. , The theory was developed in the 1970’s to produce digital filters from analog filters already being designed, developed, and prototyped.
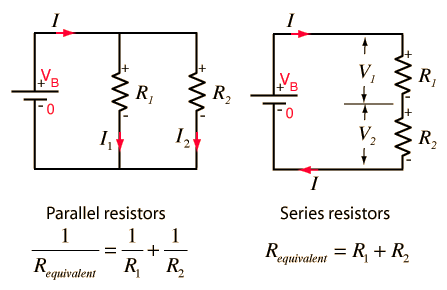In the late 1990’s the music industry revived Wave Digital Filter Theory for an entirely different reason—people loved, and wanted to mimic, the sound of analog devices. However, the types of circuits in musical devices are often complex and while Wave Digital Filter Theory is an elegant theory, it remained incomplete. The theory can only handle certain circuit topologies. Think the physical way in which all those circuit components are wired together, namely the classic series or parallel circuit. In a series circuit all the current through one electrical element flows through another element. In a parallel circuit the voltage across one electrical element is also the voltage across another electrical element. These assumptions of voltage or currents being equal are vital for solving equations of how the wave changes at each step in the circuit.
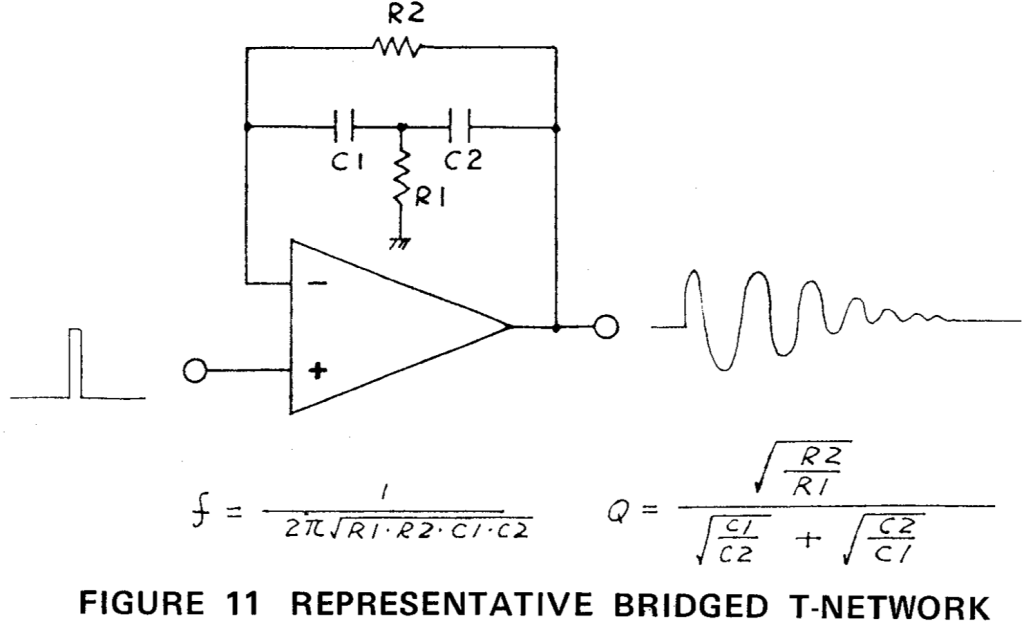But the insides of TR-808 is a cornucopia of much more complex circuits. Take the Bridged-T circuit in the 808’s kick drum, none of the elements of the circuit are in series or parallel and thus no two resistors have the same current or voltage across them. Werner’s research is making strides to actually allow Wave Digital Filter Theory to model the Bridged-T circuit and more generally an infinite number of complex circuits. To solve the Bridge-T problem, Werner borrowed from another field of mathematics called Modified Nodal Analysis. As Werner states, “Conveniently, writing out Modified Nodal Analysis equations is simple, even automatic.” But the kicker, pun intended, is that this allows for any circuit configuration to be solved because the equations are generalizable.
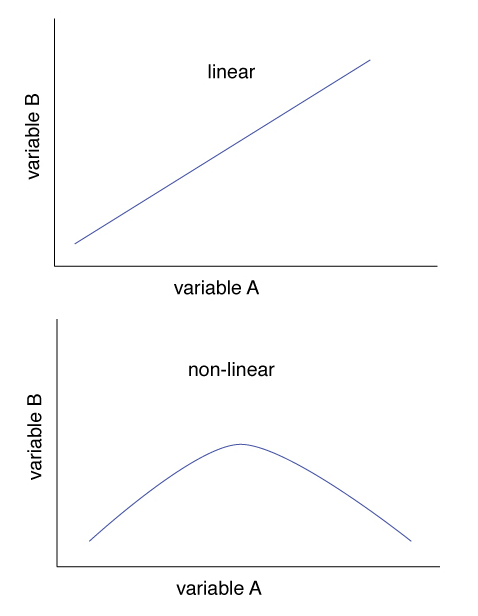However, another issue with Wave Digital Filter Theory emerges—the theory cannot handle multiple nonlinearities in the circuit. A linear relationship is where increases or decreases in variable A always cause increases or decreases in variable B. A nonlinear relationships might be where increases in variable A causes increases in variable B but only up to certain value of variable A, after which variable B decreases. The TR-808 cymbal circuit contains 21 such nonlinearities. Werner’s research solves this problem as well. Werner discovered the combination of those nonlinearities and the circuit configuration are simply a nonlinear state space system, which has its own theory of mathematics to solve.
Much like Dr. Dre’s 1992 hit Let Me Ride samples Funky Drummer by James Brown, Mothership Connection and Swing Down, Sweet Chariot by Parliament, and Kissing My Love by Bill Withers to create more than the sum of its parts, Kurt Werner is bringing together new mathematical theories to advance the field. Perhaps the advances of Wave Digital Filter Theory do not interest you, but you have to admit those theoretical advances have reproduced that beautiful 808 punch (make sure you have some good speakers or headphones). Because as the Beasties Boys rapped in Super Disco Breakin “nothing sounds quite like an 8-0-8”.